Abstract
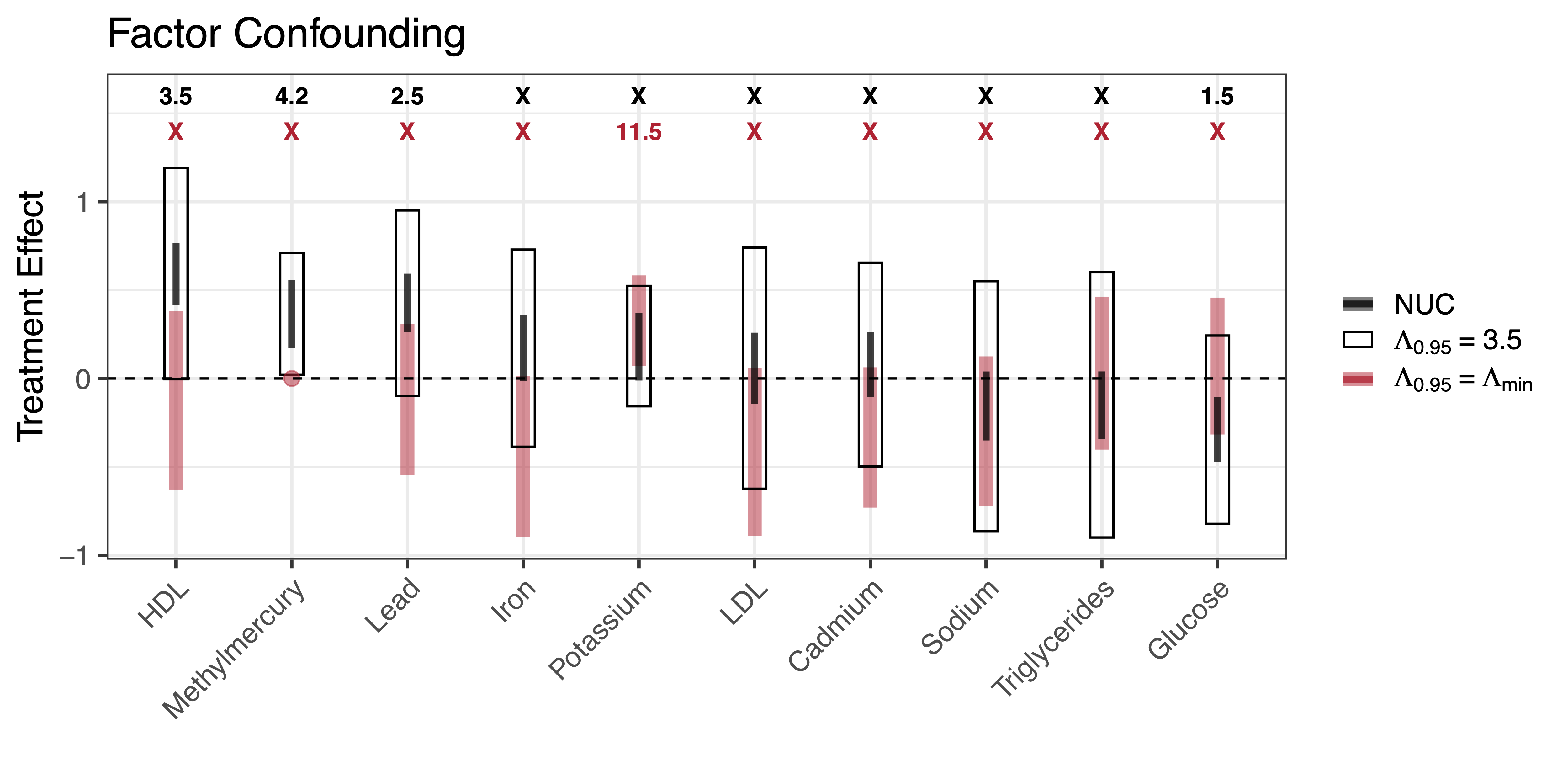
We propose an approach for assessing sensitivity to unobserved confounding in studies with multiple outcomes. Under a shared confounding assumption, we argue that it is often reasonable to use residual dependence amongst outcomes to infer a proxy distribution for unobserved confounders. We focus on a class of factor models for which we can bound the causal effects for all outcomes conditional on a single sensitivity parameter that represents the fraction of treatment variance explained by unobserved confounders. We further characterize how causal ignorance regions shrink under assumptions about null control outcomes, propose strategies for benchmarking sensitivity parameters, and derive metrics for quantifying the robustness of effect estimates. Finally, we propose a Bayesian inference strategy for quantifying uncertainty and describe a practical sensitivity workflow which we demonstrate in both simulation and in a case study using data from the National Health and Nutrition Examination Survey (NHANES).