Copula-based Sensitivity Analysis for Multi-Treatment Causal Inference with Unobserved Confounding

Abstract

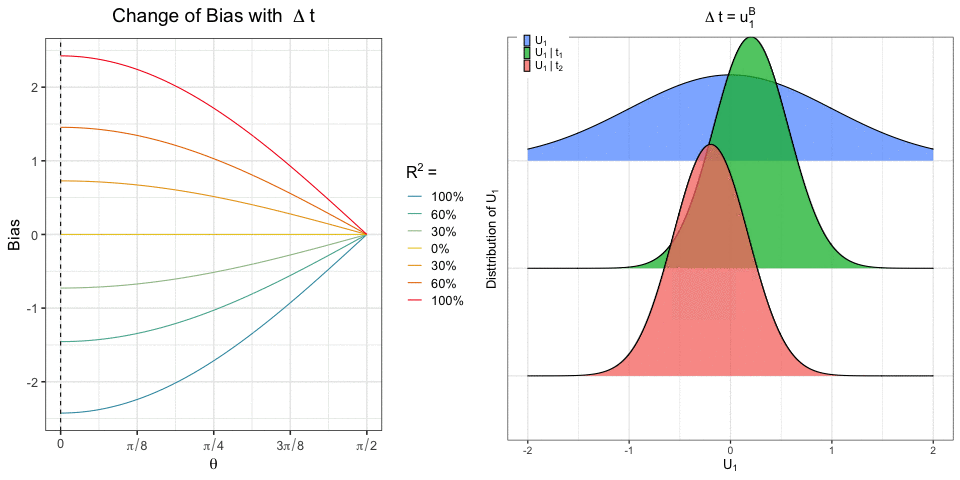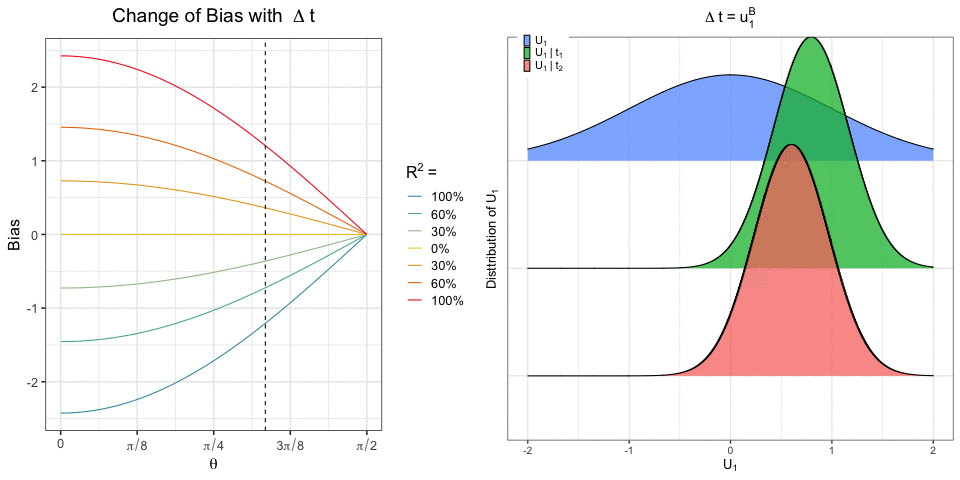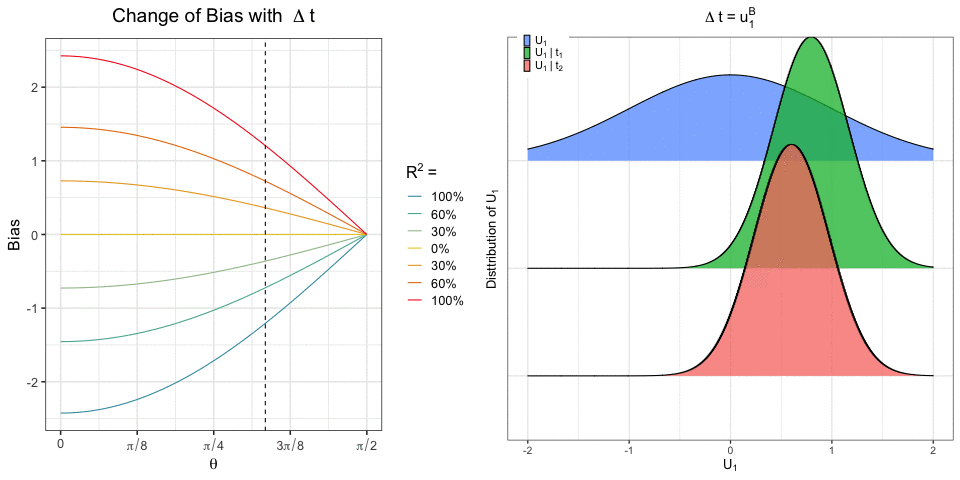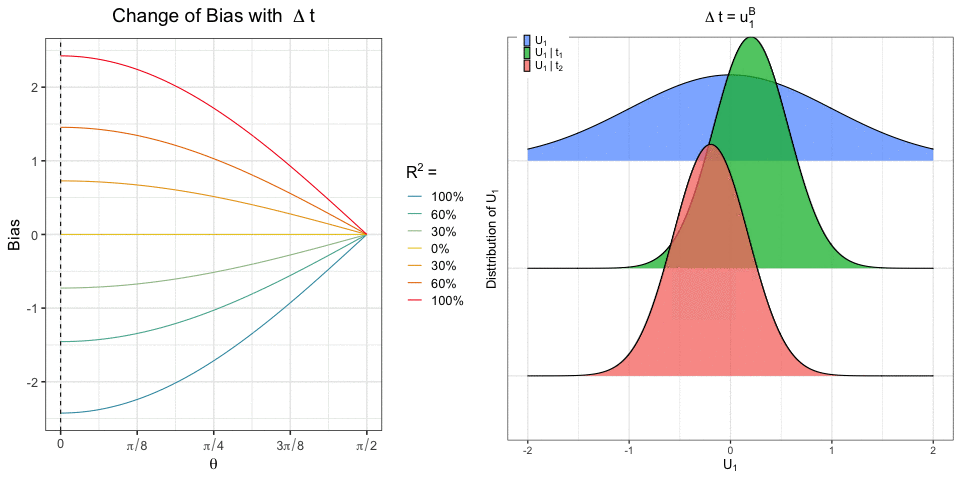
Recent work has focused on the potential and pitfalls of causal identification in observational studies with multiple simultaneous treatments. On the one hand, a latent variable model fit to the observed treatments can identify essential aspects of the distribution of unobserved confounders. On the other hand, it has been shown that even when the latent confounder distribution is known exactly, causal effects are still not point identifiable. Thus, the practical benefits of latent variable modeling in multi-treatment settings remain unclear. We clarify these issues with a sensitivity analysis method that can be used to characterize the range of causal effects that are compatible with the observed data. Our method is based on a copula factorization of the joint distribution of outcomes, treatments, and confounders, and can be layered on top of arbitrary observed data models. We propose a practical implementation of this approach making use of the Gaussian copula, and establish conditions under which causal effects can be bounded. We also describe approaches for reasoning about effects, including calibrating sensitivity parameters, quantifying robustness of effect estimates, and selecting models which are most consistent with prior hypotheses.